Data Assimilation for MHD Systems
Introduction
In this project, we utilize one of the data assimilation methods based on Monte-Carlo approximation called Ensemble Kalman Filter (EnKF), to estimate the dynamics of a two-dimensional Magnetohydrodynamic system with a good example of the turbulent phenomenon called Orszag-Tang vortex. The Orszag-Tang vortex problem shows the small scale turbulent structure induced by the magnetic field’s and plasma’s nonlinear interaction. This is a benchmark for evaluating numerical methods in plasma physics. We integrate the MHD simulation with the EnKF algorithm to estimate the dynamics of the Orszag-Tang vortex from noisy measurements and partial observations. The use of the EnKF is motivated by the fact that the integration of the Monte-Carlo method enables the reduction of the computation to estimate the error covariance by using a small ensemble of samples. This is suited for both high-dimensional and nonlinear systems with difficulties in linearizing the dynamic models, including MHD systems.
Magnetohydrodynamic System
Magnetohydrodynamics (MHD) is one of the well-known models, which assumes that the plasma is a single fluid linearly combined with the average motions of individual species based on charge-neutrality and small gyro-radius approximations. This can describe the equilibrium and large-scale dynamics of the magnetized plasma. The governing equations of MHD are derived by coupling the fluid equations with Maxwell’s equations.

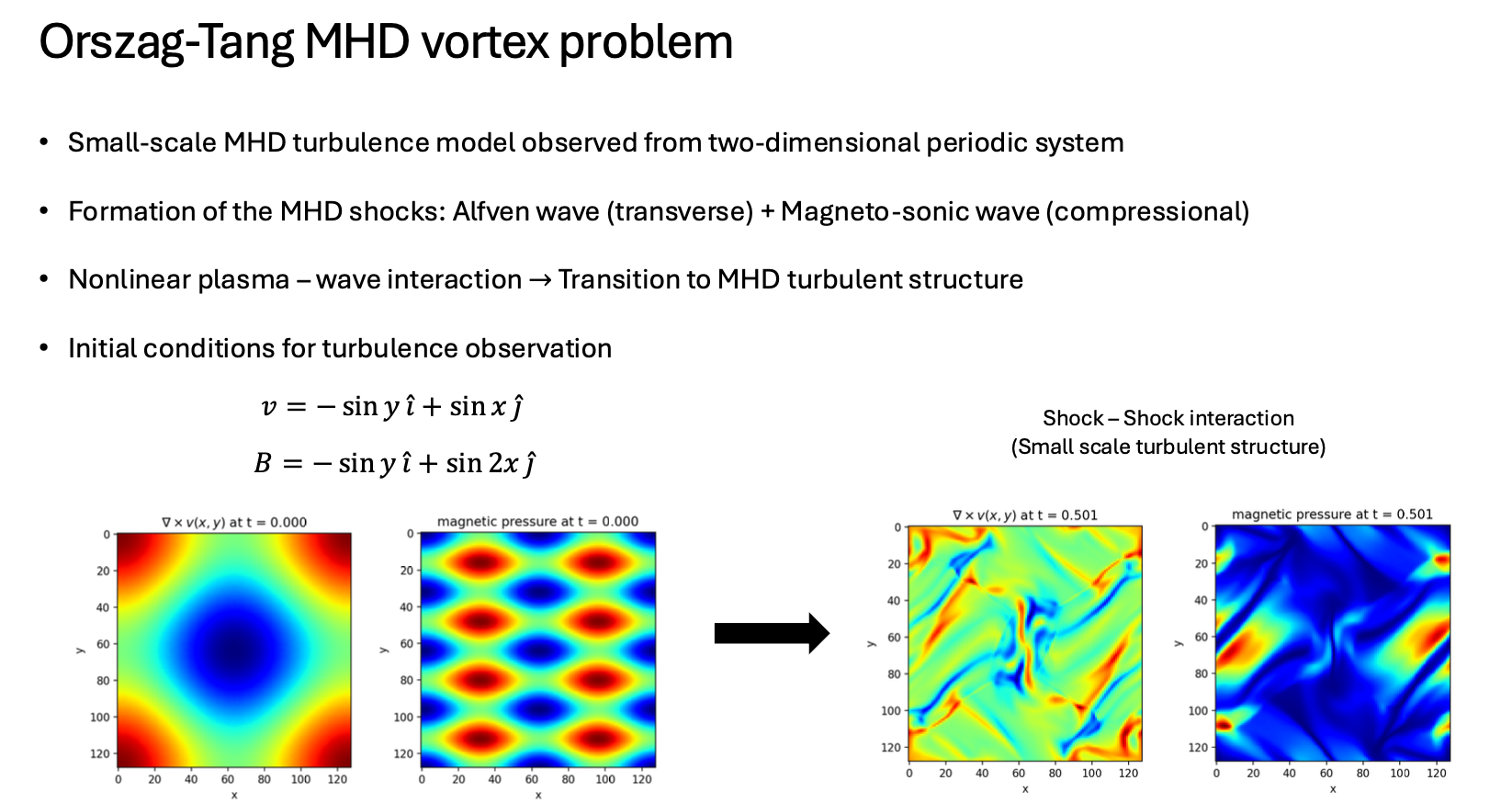
Orszag-Tang MHD vortex
A supersonic MHD turbulence model problem known as Orszag-Tang MHD vortex is observed in a two-dimensional periodic system. There is a transition to MHD turbulence when the sinusoidal perturbations in the velocity and magnetic field are applied. It is known that the nonlinear interaction between the fluid motion of the plasma and the magnetic field leads to the small-scale turbulent structure.
Ensemble Kalman Filter
Ensemble Kalman Filter(EnKF) is a Monte Carlo method based Kalman filtering, replacing the covariance required for Kalman updating by the sample covariance of the ensemble. EnKF can be a good choice for MHD since it does not require linearization for nonlinear dynamics approximation by ensemble sampling. Instead of evolving the mean and covariance matrix from the original state for each time step, the EnKF uses an ensemble of model states to approximate the covariance matrix. The overall process of EnKF is described as below.

You can see the details at the attached files.
Article
Jinsu Kim. “Data Assimilation for Orszag-Tang Magnetohydrodynamic Vortex Problem” Draft.
