Research

My research goal is to explore and foster a data-driven modeling and control in nonlinear dynamics. The main target for nonlinear dynamics is plasma system, including MHD system and Vlasov-Maxwell kinetic system. Learning dynamics from data is important for modling complex systems and can be applied to several applications for state estimation, reduced modeling, and control. The key point of learning dynamics is to bridge the gap between physics domain knowledge and data-driven modeling, and I am now focusing on how to solve this discrepancy.

Dynamics and Control

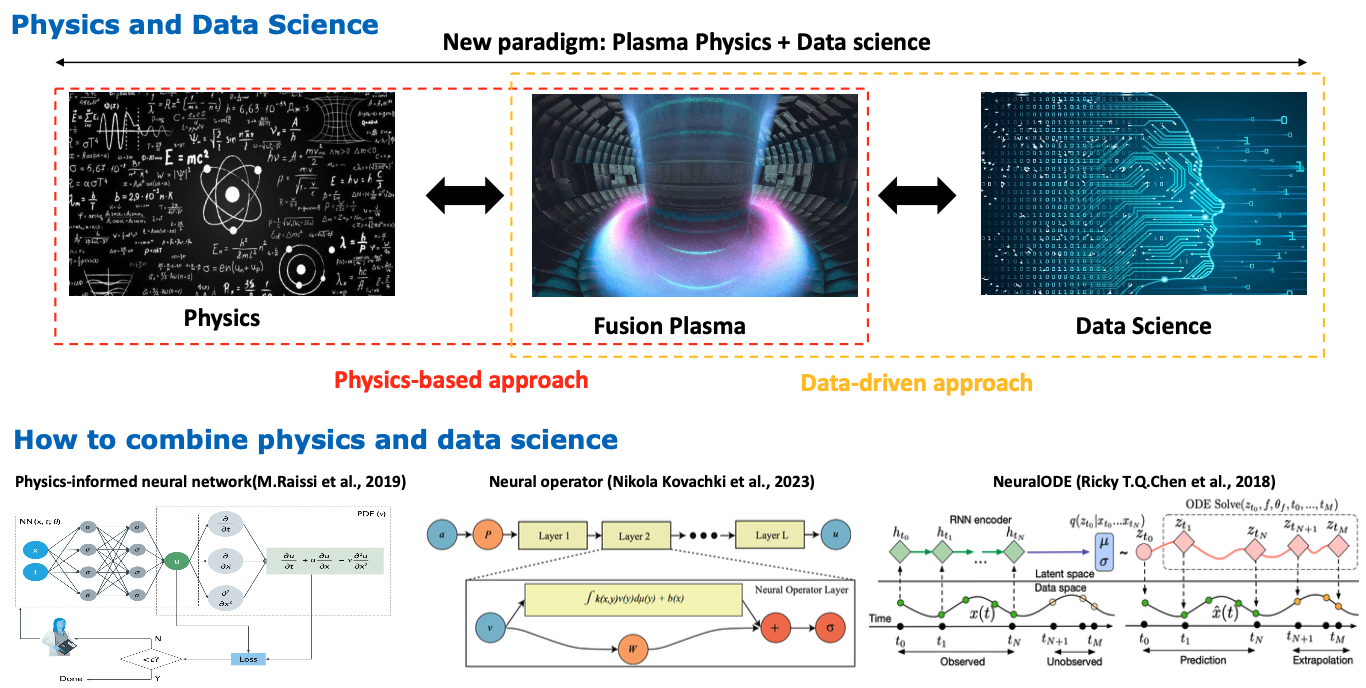
With increasing computational power and data availability, data-driven modeling and control have become essential in science and engineering. Traditional models rely on first-principles physics, often using PDEs for fluid dynamics, electromagnetism, and plasma physics. However, complex systems with nonlinear, high-dimensional behaviors challenge purely analytical approaches.

Data-driven methods leverage machine learning and optimization to infer governing equations and develop controllers from data, reducing reliance on explicit analytical models. Integrating these methods with physics-based insights has led to Physics-Informed Machine Learning (PIML), ensuring interpretability, stability, and generalizability

📌 Model reduction on nonlinear dynamic systems

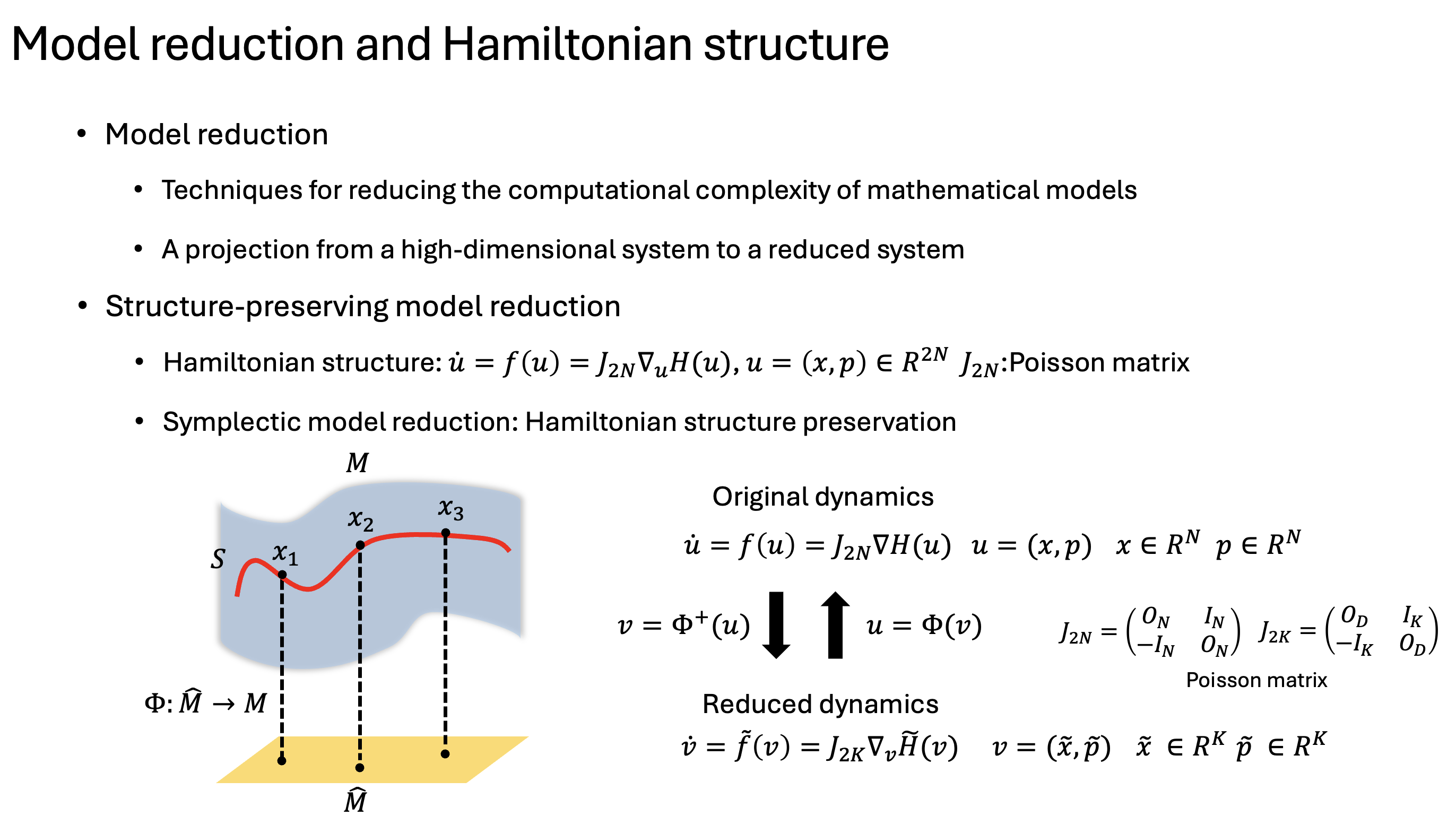
Modern simulations often involve solving mathematical models with a myriad number of variables, makeing them computationally expensive and slow to run. This is where model reduction comes in. Model order reduction is a way to build efficient and low-cost approximation for surrogate modelling. The idea is to replace the original, high-dimensional model—known as the full-order model (FOM)—with a simplified version called a reduced-order model (ROM). This ROM captures the essential behavior of the system while being dramatically faster and easier to compute.

But for the physical systems governed by conservation laws or PDEs describing the dynamics, the reduced model must preserve the underlying structure of the original systems. Symplectic model order reduction, which preserves Hamiltonian structure of the system, has been highlighted since it ensures the fundamental geometry of Hamiltonian systems, preserving the stability, accuracy, and conservation of the energy during the simulation. Extension to nonlinear systems preserving Hamiltonian structure has been studied and the primary goal of this research is to apply the structure-preserving model order reduction into the plasma kinetics, one of the good examples of nonlinear dynamics for verification.

Plasma Dynamics

Plasma is the fourth state of matter, consisting of a partially ioniszed gas of ions, electrons, and neutral particles. Plasma dynamics describes how these charged particles interact under electric and magnetic fields, leading to collective behavior unlike neutral gases. This results in unique phenomena such as plasma waves, instabilities, and turbulence.

One fundamental framework for describing plasma behavior is magnetohydrodynamics (MHD), treating plasma as a conducting fluid and combines fluid equations with Maxwell’s equations. However, many plasmas exhibit kinetic effects that require a more detailed description based on the Boltzmann equation and the Vlasov-Maxwell system.

📌 Computational plasma physics

Simulating the dynamics of charged particles in a plasma is a challenging task, especially because these systems live in high-dimensional phase space and involve complex interactions. One widely used technique in computational plasma physics to tackle this challenge is the Particle-In-Cell (PIC) method.

The Particle-In-Cell (PIC) method is a widely employed numerical technique in computational plasma physics, particularly well-suited for simulating collisionless kinetic systems. It combines a Lagrangian treatment of particles—tracking their evolution in phase space—with an Eulerian discretization of fields and source terms on a fixed spatial mesh. This hybrid framework allows for a significant reduction in computational cost compared to direct simulation of high-dimensional kinetic equations, while still capturing essential particle-field interactions.

In PIC approach, the plasma distribution function is discretized by Klimontovich representation. Each particle contributes to charge and current densities via interpolation to the mesh, enabling the solution of Maxwell’s or Poisson’s equations on the grid. The resulting fields are then interpolated back to the particle locations to update their trajectories. This iterative cycle enables the PIC method to resolve fine-scale kinetic effects and collective plasma behavior simultaneously.

A simplified case of PIC with one-dimensional electrostatic plasma is developed to investigate the kinetic pheonmena such as two-stream instability and bump-on-tail instability. Application of the symplectic model order reduction based on PIC simulation is now being proceeded.

📌 Plasma disruption prediction with data-driven approaches in fusion reactor device

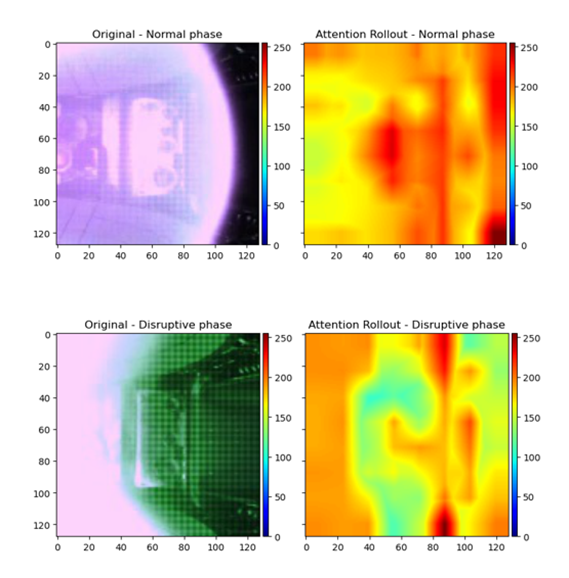
Plasma disruption is a major challenge in fusion plasma, requiring accurate prediction to maintain stable operation and prevent damage. Disruptions in tokamak plasmas involve a sudden loss of plasma, releasing massive energy and particles that can severely impact the reactor. During a thermal quench, the rapid collapse of plasma thermal energy increases the toroidal electric field, leading to the formation of runaway electrons. These high-energy electrons can strike plasma-facing components such as walls and divertors, causing erosion, melting, or structural damage. Additionally, the abrupt loss of plasma energy and current induces mechanical forces on the vessel, further stressing the device.

To mitigate these risks, early and accurate disruption prediction is essential. A reliable prediction system must achieve high precision and recall, minimizing missed alarms and false positives for practical application in fusion reactors. Our research explores data-driven approaches, including deep learning and Bayesian modeling, to enhance disruption forecasting in real device. By leveraging multimodal diagnostics and uncertainty quantification, these methods improve predictive reliability, contributing to safer and more efficient plasma operation.

📌 Data-driven modeling and optimized control for fusion plasma operation

Achieving stable, high-performance plasma in steady-state fusion reactor operations is a complex challenge due to competing constraints, such as operational limits and instabilities. Traditional experimental trials alone are inefficient in optimizing plasma conditions, as they rely heavily on manual adjustments and predefined models.

Reinforcement learning (RL) offers a promising alternative by enabling adaptive, data-driven, and model-free control. Unlike conventional approaches, RL can autonomously explore optimal plasma trajectories without requiring precise mathematical models. Moreover, Multi-Objective reinforcement learning (MORL) can allow simultaneous control of multiple plasma parameters for stable and high-performance plasma.

Combined with the Grad-Shafranov Physics-Informed Neural Network (GS-PINN) simulator, the plasma response with respect to RL-driven control with EC heating, coil currents, and magnetic field are now able to be approximated. The potential of data-driven plasma modeling and control for avodiing plasma instabilities is a next step of this reserach.

📌 Design optimization of a tokamak fusion reactor with data-driven approaches

Designing a nuclear fusion reactor requires balancing multiple physics and engineering constraints to achieve steady-state operation while minimizing costs. Traditional optimization approaches struggle with the complexity of these competing factors, making efficient reactor design a significant challenge.

This research applies Deep Reinforcement Learning (DRL) to streamline fusion reactor design optimization. By leveraging parallelizable optimization algorithms, DRL enables efficient exploration of design parameters, identifying optimal configurations that meet operational requirements while reducing construction costs.

The proposed multi-objective DRL framework simplifies reactor design by autonomously navigating trade-offs between performance and feasibility. This demonstrates the potential of AI-driven optimization for advancing the development of efficient and sustainable fusion reactors.